Permutations and Combinations

Overview

Teaching: min
Exercises: min

Questions

• what are permutations and combinations

Objectives

• Apply Fundamental Counting Principle

• Apply Permutations

• Apply Combinations

Concepts / Definitions

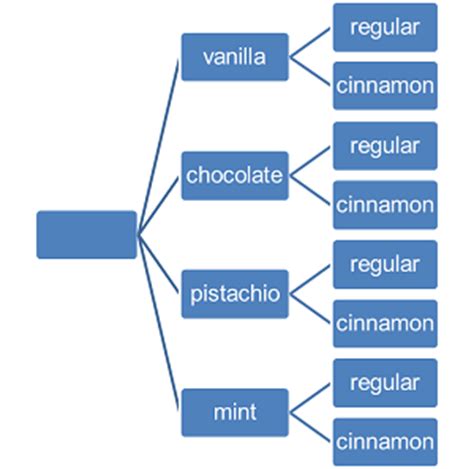
The Fundamental Counting Principle states that if one event has \(m\) possible outcomes and a second independent event has \(n\) possible outcomes, then there are \(m\) x \(n\) total possible outcomes for the two events together.

If you have four flavors of ice cream and two types of cones, then ther are \(4 * 2 = 8\) possible combinations.

In mathematics, the factorial of a non-negative integer \(n\), denoted by \(n!\), is the product of all positive integers less than or equal to \(n\). \(n! = n(n-1)(n-2)(n-3)\ ...\ (2)(1)\) By definition, \(0! = 1\).

Permutations are the number of ways a set of \(n\) distinguishable objects can be arranged in order.
\(4!\) = 24 ways to order four items

The number of permutations on \(n\) objects taken \(r\) at a time is given by \(P\binom{n}{r} = P(n, r) = nPr = \frac{n!}{(n-r)!}\)

The number of ways \(n\) items can be ordered with replacement \(r\) times is \(n^r\)

\(\frac{4!}{(4-3)!}\) = 24 ways of selecting and ordering 3 or 4 letters, but only 4 ways if order does not matter.

Combinations are the number of ways selecting \(r\) items from a group of \(n\) items where order does not matter.
To take out all the ways \(r\) can happen, we divide out all the ways \(r!\) can happen.
The number of combinitions of \(n\) objects taken \(r\) at a time is given by \(C\binom{n}{r} = C(n, r) = nCr = \frac{n!}{r!(n-r)!}\) \(\implies\) Also called \(n\) choose \(k\), noted \(\binom{n}{k} = \frac{n!}{k!(n-k)!}\)

Counting Subsets of an \(n\)-Set
Consider a binomial situation, where there is a yes or no, success or failure, possibility happening \(n\) times. The number of ways this can happen is \(2^n\). There are \(2^n\) subsets of a set with \(n\) objects.

Exercises

1. A four-volume work is placed in random order on a bookshelf. What is the probability of the volumes being in proper order from left to right or from right to left?

Solution

If you have four volumes, and the question is what order to place them in, the question is a simple permutation problem. There are 4 possibilities for the first, 3 for the second, 2 for the third and only one for the last, making the number of permutations of the books 24. Only one order has them in ascending order and only one order will have them in descending order. Thus: \(P=\frac{2}{24}=\frac{1}{12}\label{answer1.1}\)

2.A wooden cube with painted faces is sawed up into 1000 little cubes, all of the same size. The little cubes are then mixed up, and one is chosen at random. What is the probability of its having just 2 painted faces?

Solution

The wooden cube is made of \(10^3\) cubes implying a 10x10x10 cube. The cubes that have two faces painted will be the edges which are not on a corner. Thus, since there are 12 edges of 10 cubes each, 8 of which are not corners, that implies we have 96 edges. 96 thus becomes our number of desireable outcomes and 1000 has always been the total number of outcomes: \(P=\frac{96}{1000} = 0.096\label{answer1.2}\)

3. A batch of n manufactured items contains k defective items. Suppose m items are selected at random from the batch. What is the probability that l of these items are defective?

Solution

If there are \(n\) total items and \(k\) of them are defective. We select \(m\) and want to know the probability of \(l\) of them being defective ones. There are \(\binom{n}{m}\) possible ways to chose \(m\) different items from the population of \(n\) items which will be our denominator. Now we need to know how many of those possibilities have \(l\) bad ones in them for our numerator. If there’s \(k\) total defective ones, then there are \(\binom{k}{l}\) \(P = \frac{\binom{k}{l}}{\binom{n}{m}}\label{answer1.3}\)

4. Ten books are placed in random order on a bookshelf. Find the probability of three given books being side by side.

Solution

There are \(10!\) possible ways to order the ten books. You can imagine that since the three books have to take up three adjacent positions, there are 8 possible locations for the three books to be ordered. Taking just the first position (that being the first three “Slots”), there are 6 ways to order the desired books and then \(7!\) ways to order the remaining books. Thus there are \(8 \cdot{} 6 \cdot{} 7!\) desirable orders giving us a probability of \(P=\frac{8 \cdot{} 6 \cdot{} 7!}{10!}=\frac{1}{15}\label{answer1.4}\)

5. One marksman has an 80% probability of hitting a target, while another has only a 70% probability of hitting the target. What is the probability of the target being hit (at least once) if both marksman fire at it simultaneously?

Solution

There are 4 possibilities to consider here: neither hits, one or the other hits and both hits. While it may be tempting to calculate the probability of each event, since we only care about the probability of at least one hitting the target, we need only calculate the probability that no one hits and subtract that from 1. The first marksman has an \(.8\) probability of hitting meaning he has a missing probability of .2; similarly the second marksman has a .7 chance of hitting and a .3 chance of missing. Thus, the probability of both one and two missing is the product of the two missing probabilities: \(.2*.3=.06\) \(P=1-.06=.94\label{answer1.5}\)

6. Suppose n people sit down at random and independently of each other in an auditorium containing n + k seats. What is the probability that m seats specified in advance (m < n) will be occupied?

Solution

The total number of ways \(n+k\) seats can be occupied by \(n\) people is \(\binom{n+k}{n}=\frac{(n+k)!}{n!k!}\) but once again the difficult part is finding the total number of desirable outcomes. If you were to specify \(m\) seats, you effectively divide the auditorium into two buckets so we need to find the number of ways to partition people into those two buckets which will give us the numerator, \(\binom{n+k}{m}=\frac{(n+k)!}{m!(n+k-m)!}\)
\(P=\frac{(n+k)!}{m!(n+k-m)!}\frac{n!k!}{(n+k)!}\)
\(=\frac{n!k!}{m!(n+k-m)!}\)

7. Three cards are drawn at random from a full deck. What is the probability of getting a three, a seven and an ace?

Solution

Again, the number of ways to get three cards from a 52 card deck is \(\binom{52}{3}\). Since there are 4 each of sevens, threes and aces, there are $4^3$ desirable hands. \(P=\frac{4^3}{\frac{52!}{3!49!}}=\frac{16}{5525}=0.00289593 \label{answer1.7}\) Which it is worth pointing out, is no different than any other 3-card hand of three different cards.

8. What is the probability of being able to form a triangle from three segments chosen at random from five line segments of lengths 1, 3, 5, 7 and 9?

Hint. A triangle cannot be formed if one segment is longer than the sum of the other two.

Solution

If you indiscriminately chose 3 line segments from our bank of 5, you have \(\binom{5}{3}=10\) total possibilities for triangles.
When you look at the bank \((1, 3, 5, 7, 9)\), however, you have to make sure that no two segments are longer than the third segment, otherwise making a triangle is impossible.
The brute-force way to do this is start with 1 and realize there’s no triangle that can be formed with 1.
Then, looking at 3, you realize that you can do \((3, 5, 7)\) and \((3, 7, 9).\ Starting now with 5, you can do only\)(5, 7, 9)\(\ At this point, you realize you're done and that the answer is plain to see\)P=\frac{3}{10}=.3\label{answer1.8}$$

9. Suppose a number from 1 to 1000 is selected at random. What is the proba­bility that the last two digits of its cube are both 1?

Hint There is no need to look through a table of cubes.

Solution

We could do this problem in 5 minutes of programming and an instant of computation but that’s not the point! We need to think our way through this one. How many cubes of the numbers between 1 and 1000, have 11 for the last two digits. Luckily, each cube is unique so there’s no complications there: only 1000 possibilities. Let’s break down the number we’re cubing into two parts, one that encapsulates the part less than 100 and then the rest of the number \(n=a+b=100c+b\) Now, just for fun, let’s cube than number \(n^3=(100c+b)^3=b^3+300 b^2 c+30000 b c^2+1000000 c^3\) Clearly the only term here that will matter to the last two digits of the cube is \(b\), the part less than 100. Now we can reduce our now size 100 subspace by a great deal if you realize that in order for a number’s cube to end in 1, the last number in the cube will need to be 1, leaving us: (1, 11, 21, 31, 41, 51, 61, 71, 81, 91). At this point I recommend just cubing all the numbers and realizing that only \(71^3=357911\) fulfills the requirements giving only one desirable outcome per century(71, 171, 271 etc.) \(P=\frac{10}{1000}=.01\label{answer1.9}\)

10. Find the probability that a randomly selected positive integer will give a number ending in 1 if it is

a) Squared ; b) Raised to the fourth power; c) Multiplied by an arbitrary positive integer. Hint. It is enough to consider one-digit numbers.

Solution

Now we want to know about all positive integers but just the last digit and the probability that the last digit is one. To prove that we can use the hint given, we’ll split the integer into the past less than 10 and the part greater than 10. \(n=10a+b\)

a–Squared

\(n^2=100a^2+10ab+b^2\) OK, so clearly only \(b^2\) contributes to the last digit. At this point... just do the squaring especially since it’s something you can do in your head. (1, 2, 3, 4, 5, 6, 7, 8, 9)\(\rightarrow\)(1, 4, 9, 16, 25, 36, 49, 64, 81) therefore there are two desireable outcomes for every decade of random positive integers.
\(P=\frac{2}{10}=.2\)

b–fourth-powered

\(n^4=100000000 a^4+4000000 a^3 b+60000 a^2 b^2+400 a b^3+b^4\) Great, once again, just \(b^4\). Now, doing the forth power is a little harder so let’s reason through and reduce the subspace. Clearly, only odd numbers will contribute since any power of an even number is again an even number. Now, let’s just do the arithmetic. (1, 3, 5, 7, 9)\(\rightarrow\)(1, 81, 625, 2401, 6561) giving us 4 desirable outcomes per decade of random numbers
\(P=\frac{4}{10}=.4\)

c–multiplied by random positive number

\(n*r=(10a+b)r\) Now let’s let $r$ be a similar integer as n \(n*r=(10a+b)(10c+d)=100ac+10(bc+ad)+bd\) So we just need to consider the first two digits of both the random number and the arbitrary number. This leaves us with $10^2$ possibilities; \(5^2\) possible desirable outcomes once we exclude even numbers: (1, 3, 5, 7, 9). Once again we resort to brute force by just defining the above as a vector and multiplying the transpose of that vector by the vector. The only desirable outcomes turn out to be (1*1, 9*9, 7*3, 3*7), giving four desirable outcomes per century.
\(P=\frac{4}{100}=.04\)

11. One of the numbers 2, 4, 6, 7, 8, 11, 12 and 13 is chosen at random as the numerator of a fraction, and then one of the remaining numbers is chosen at random as the denominator of the fraction. What is the probability of the fraction being in lowest terms?

Solution

Here we are given 8 possible numbers (2, 4, 6, 7, 8, 11, 12, 13) and are told that it making a random fraction out of two of the numbers. There are \(\binom{8}{2}=28\) possible pairs but since \(\frac{a}{b} \neq \frac{b}{a}\), we multiply that by two to get the total number of fractions we can get from these numbers as being 56. Looking at the numbers given, 7, 11 and 13 are all prime and all the others are divisible by two; therefore only the fractions that contain one or more prime numbers will be in lowest terms. The number 7 can be in 7 different pairs with the other numbers which makes for 14 fractions. 11 can be in 6 pairs or 12 fractions (since we already counted 7) and similarly, 13 can be in 10 uncounted fractions giving 36 possible fractions in lowest terms.
\(P=\frac{36}{56}=\frac{9}{14}\label{answer1.11}\)

12. The word “drawer” is spelled with six scrabble tiles. The tiles are then randomly rearranged. What is the probability of the rearranged tiles spelling the word “reward?»

Solution

The word drawer has 6 letters and there are \(6!=720\) possible ways of arranging the letters. It is then natural to say there’s only one way to spell reward correctly and thus the probability of spelling it correctly after a random reordering is \(1/720\) BUT there is a complication in that the two of our letters are the same, meaning there are to distinct arrangement of our distinguishable tiles that will give us the proper spelling. \(P=\frac{2}{720} = \frac{1}{360}\label{answer1.12}\)

13. In throwing 6n dice, what is the probability of getting each face n times? Use Stirling’s formula to estimate this probability for large n.

Solution

For any die, there are 6 different possibilities. Since one dice’s outcome does not depend on another’s, that means that for a roll of \(6n\) die, there are \(6^{6n}\) different possible outcomes for the dice rolls. Now for desirable outcomes, we want each of the 6 faces to show up n times. To accomplish this, we just count the number of ways to apportion \(6n\) things into 6 groups of $n$ each or \(\frac{(6n)!}{(n!)^6}\) which, given Stirling’s approximation \(n! \approx \sqrt{2 \pi n} n^n e^{-n}\) gives us for large \(n\) \(\frac{(6n)!}{(n!)^6} \approx \sqrt{2 \pi 6n} (6n)^{6n} e^{-6n} * \frac{1}{(\sqrt{2 \pi n} n^n e^{-n})^6} = \frac{3 \cdot 6^{6n}}{4 (\pi n)^{5/2}}\) \(P=\frac{(6n)!}{(n!)^6 6^{6n}} \approx \frac{3}{4 (\pi n)^{5/2}}\label{answer1.13}\)

14. A full deck of cards is divided in half at random. Use Stirling’s formula to estimate the probability that each half contains the same number of red and black cards.

Solution

To figure out the total number of possibilities, we must realize that one draw of half a deck, implies the other half of the deck implicitly, therefore there are \(\binom{52}{26}\) total 26 card draws. Then, to get 13 red cards, there are \(\binom{26}{13} = 10400600\) ways to get 13 red cards and the same number for black cards making $10400600^2$ the number of total possible desirable outcomes.
\(P=\frac{16232365000}{74417546961}=0.218126\)
Because we’re cool and modern and have Mathematica, we don’t NEED to do the Stirling’s formula approximation but it’ll be good for us so we shall.
\(P=\frac{\binom{26}{13}^2}{\binom{52}{26}} = \frac{(26!)^4}{(13!)^4 52!}=\frac{((2n)!)^4}{(n!)^4 (4n)!}\) where \(n=13\).
\(P=\frac{(\sqrt{4 \pi n}(2n)^{2n}e^{-2n})^4}{(\sqrt{2 \pi n}n^{n}e^{-n})^4 (\sqrt{8 \pi n}(4n)^{4n}e^{-4n})}\)
\(P=\frac{(4 \pi n)^2}{(2 \pi n)^2 \sqrt{8 \pi n}} \frac{(2n)^{8n}}{n^{4n}(4n)^{4n}} = \frac{4}{\sqrt{8 \pi n}} \frac{2^{8n}}{4^{4n}}\)
\(P=\frac{2}{\sqrt{26 \pi}} = 0.221293\) which when you take the ratio of approximate to exact, you get $1.01452$ so the approximation is less than \(2\%\) off... not bad!

15. Use Stirling’s formula to estimate the probability that all 50 states are represented in a committee of 50 senators chosen at random.

Solution

There are 100 senators at any given time. Much like the previous problem, there are \(\binom{100}{50}=100891344545564193334812497256\) different 50 senator committees. Much like the previous problem, there are \(\binom{2}{1}=2\) ways for California to be represented on the committee making for 50 states \(2^{50}\) possible even committees \(P=\frac{2^{50}}{\binom{100}{50}} = \text{1.115952921347132$\grave{ }$*${}^{\wedge}$-14}\label{answer1.15}\)

16. Suppose 2n customers stand in line at a box office, n with 5-dollar bills and n with IO-dollar bills. Suppose each ticket costs 5 dollars, and the box office has no money initially. What is the probability that none of the customers has to wait for change?

Solution

For \(2n\) people, there are \((2n)!\) different possible lines; we want the number of lines where at any given point in the line, there are more people with 5 dollar bills than 10 dollar bills. The given reference (freely available on Google books) has a fascinating geometrical argument about how \(\binom{2n}{n+1}\) is the number of lines that have one or more too many people with tens in front of people with fives. Also, in this argument, there are \(\binom{2n}{n}\) trajectories instead of \((2n)!\) lines. \(P=\frac{\binom{2n}{n}-\binom{2n}{n+1}}{\binom{2n}{n}} = \frac{1}{n+1}\label{answer1.16}\)

17. Prove that \(\sum_{k=0}^{n} {n \choose k} ^{2} ={n \choose 2} ^{n}\)

Hint. Use the binomial theorem to calculate the coefficient of \(x^{n}\) in the product \((1 + x)^{n} \cdot (1 + x)^{n} = (1 + x)^{2n}\).

Solution

We wish to prove that \(\sum_{k=0}^{n} \binom{n}{k}^2 = \binom{2n}{n}\label{answer1.17}\)
This is easies if we listen to the hint and consider that
\(\binom{2n}{n}\) is the coefficient of \(x^n\) in the polynomial
\((x+1)^{2n}\) which is also equivalent to \((x+1)^n(x+1)^n\)
We make use of: \((x+1)^n = \sum_{k=0}^{n} \binom{n}{k} x^k\)
\((x+1)^n(x+1)^n = \sum_{k=0}^{n}\sum_{j=0}^{n} \binom{n}{k} \binom{n}{j} x^k x^j\)
We want the \(x^n\) term: where \(k+j=n\) or, put another way, where
\(k=n-j\)... \(\sum_{j=0}^{n} \binom{n}{n-j} \binom{n}{j} = \sum_{j=0}^{n} \frac{n!}{j!(n-j)!}\frac{n!}{(n-j)!j!} = \sum_{j=0}^{n} \binom{n}{j}^2\)

Exercises

1. How many ways can 8 runners in a track race finish?
2. Subway is running a special on 6” subs for $3.99 with 6 choices of bread, 3 choices of meat, and 2 choices of cheese. Not including toppings or sause, how many choices are available?
3. How many ways can 2 students of a class of 25 be selected for room reps?
4. How many distinguishable ways can the letters, TOPPINGS be written?
5. A license plate has 3 letters followed by 3 digits. How many possible plates are there?
6. From a group fo 10 people in theater, how many possible ways can a teacher select roles for a show on the 7 dwarfs?
7. In the original version of poker, straight poker, a five-card hand is dealt from a standard deck of 52. How many different hands are possible?
8. A coin is flipped 10 times, and the sequence is recorded.
   1. How many sequences are possible?
   2. How many sequences have exactly 7 heads?
9. A particular subway advertises 256 ways for a sandwich to be fixed with veggies. How many veggie toppings does this subway offer?
10. Calculate \(_{10}C_3\) without a calculator.

Key Points